rsa 初步学习笔记

2025-08-09
#ctf #crypto #rsa

1 因数，质数，余数

2 公钥，私钥
1）制作过程：

2） 实际操作过程：

3 具体题目解题过程中获得知识点
1）克拉默法则：
功能：确定线性方程组是否有解，以及解的唯一性。
重点！！！：只适用于方程组中未知量个数与方程个数相等的情形（具体原因？
基本形式：如果线性方程组的系数行列式不等于零，那么该方程组一定有唯一解。这个行列式可以通过将线性方程组的右端项b1, b2, …, bn分别代入原行列式的相应列元素中得到。
定理与推论：
定理1：如果线性方程组的系数行列式D不等于零，那么该方程组一定有唯一解。
定理2：如果线性方程组无解或有多个不同的解，那么它的系数行列式D必为零。
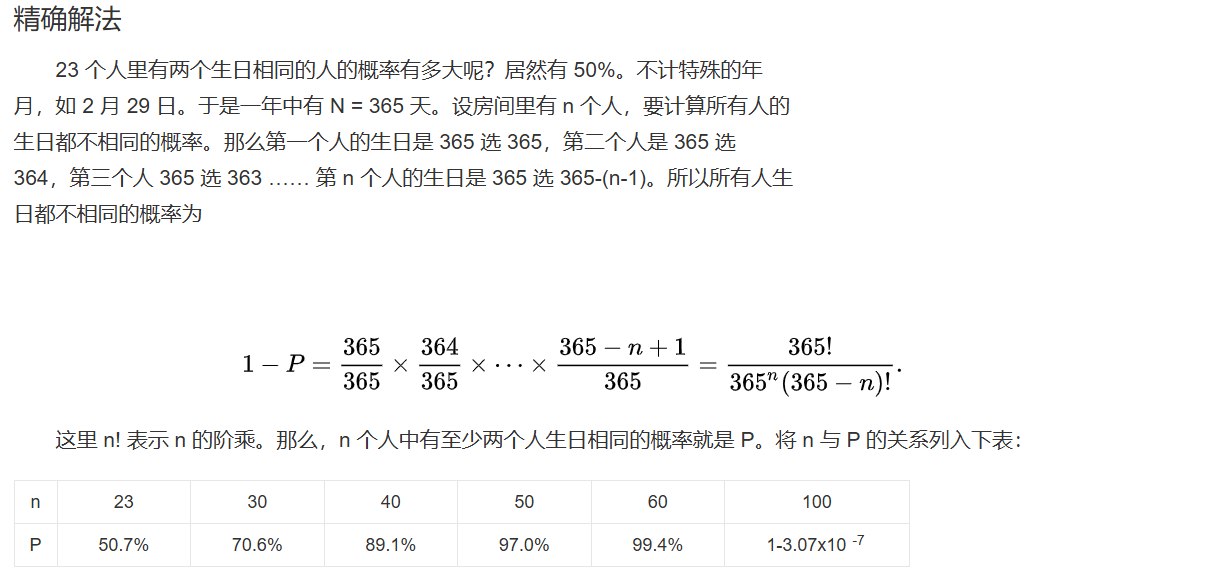
2）生日悖论


3）Floyd判圈算法（又称龟兔赛跑算法）
1 应用：
· 检测是否存在环
· 若环存在，可以计算出环的长度
· 若环存在，可以计算出环的起点
2 算法原理证明：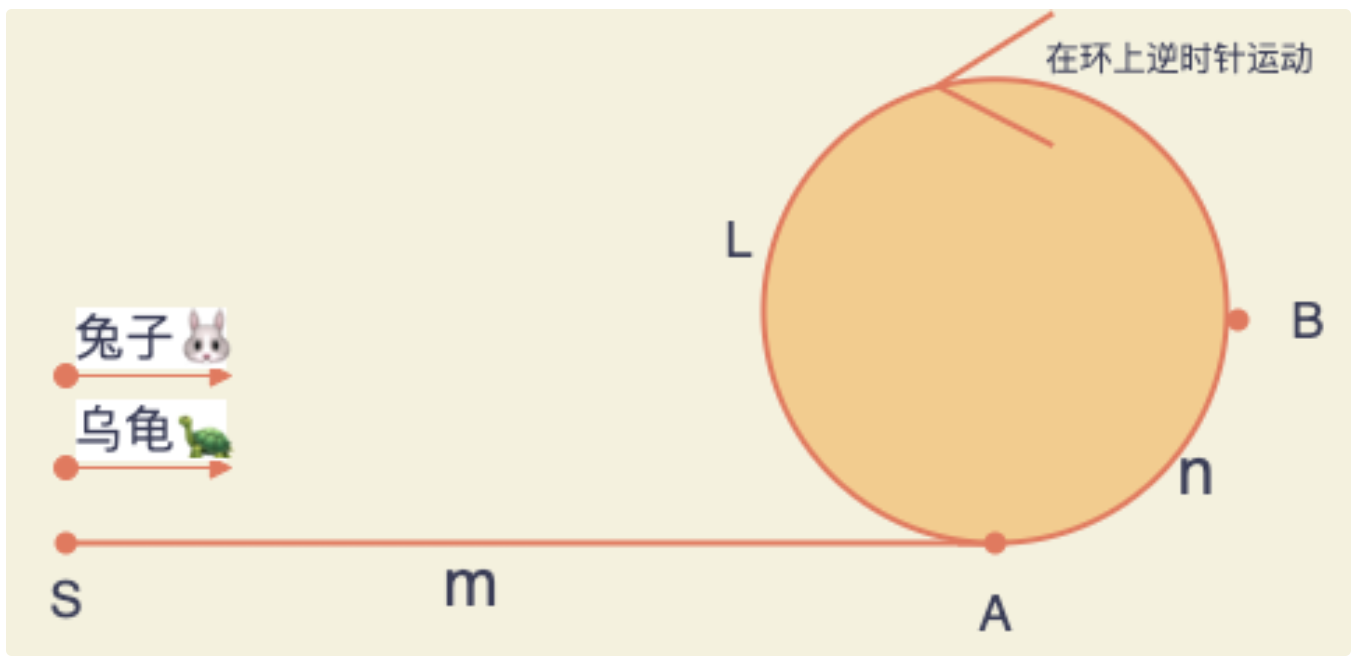

如图1 已知兔子和乌龟同时从链表起点S出发，兔子速度是乌龟的两倍（乌龟每次向后移动1步，兔子移动每次向后移动2步），m是S和A之间的距离，n是A和B之间的距离，A是环的起点，L是环的长度，B是兔子、乌龟第一次相遇的点。

  1. 环是否存在
    结论：若兔子在达到链表尾部前，乌龟与兔子相遇了，则说明链表有环。
    反证法：若环不存在，那么乌龟永远追不上兔子，那么在兔子到达链表尾部前乌龟不会和兔子相遇。若相遇了，则链表有环。
  2. 求环的长度
    已知乌龟和兔子相遇时，它们必定都在环上。设它们第一次相遇在B点，相遇后兔子保持不动，乌龟保持每次移动一步的速度继续前行，第二次相遇时，环长度L=第一次相遇后到第二次相遇时乌龟走过的路程。
  3. 求环的起点
    设乌龟走过的全部路程为i，那么有
    i = m + n + aL （1）「a是乌龟绕过的环的圈数」
    因为兔子的速度是乌龟的两倍，所以有
    2i = m + n + bL（2）「b是兔子绕过的环的圈数」
    (2) – (1)可得：
    i = (b – a)L （3）
    结合式子(1)、(3)可得 m + n + aL = (b – a)L，所以有
    m + n = (b-2a)L（4）{因为m+n>0且L>0, 所以b-2a>=1}
    所以可以得出结论：m + n = 环长度L的正整数倍。（5）
    当乌龟和兔子在B点第一次相遇后，让乌龟回到起点S，兔子仍在B，乌龟以每次1步的速度向前走，兔子以相同的速度绕环逆时针前进。当走了m步时，兔子和乌龟都正好在A处，即环的起点。因为兔子相对于A点走了(n+m)步，由结论(5)可知A必然是环的起点。【不懂】

4 具体题目解题过程中获得工具
1）https://factordb.com/
分解n工具，注意！！！点数字后就到上方框里了可以复制！！！（有点愚蠢但愚蠢的人没发现

具体题目：
· 来源：spc学长xc
基础rsa，在python中使用inverse()函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#from Crypto.Util.number import *
#from secret import flag
#m = bytes_to_long(flag)
#p = getPrime(512)
#q = getPrime(512)
#e = 65537
#n = p*q
#c = pow(m,e,n)
#print(f'p = {p}')
#print(f'q = {q}')
#print(f'c = {c}')

p = 12567387145159119014524309071236701639759988903138784984758783651292440613056150667165602473478042486784826835732833001151645545259394365039352263846276073
q = 12716692565364681652614824033831497167911028027478195947187437474380470205859949692107216740030921664273595734808349540612759651241456765149114895216695451
c = 108691165922055382844520116328228845767222921196922506468663428855093343772017986225285637996980678749662049989519029385165514816621011058462841314243727826941569954125384522233795629521155389745713798246071907492365062512521474965012924607857440577856404307124237116387085337087671914959900909379028727767057

#最终解决方法：
from Crypto.Util.number import long_to_bytes, inverse
e = 65537          
n = p * q
t = (p - 1) * (q - 1)
d = inverse(e, t)
m = pow(c, d, n)

flag = long_to_bytes(m)
print(flag.decode())

· 来源：spc学长xc
题目提示：大数N的分解
题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from Crypto.Util.number import *
from gmpy2 import *
from serct import flag
p = getPrime(512)
q = getPrime(512)
n = p*q
m = bytes_to_long(flag)
e = 65537
c = powmod(m, e, n)#加密结果    
print(n)
print(c)

# 52147017298260357180329101776864095134806848020663558064141648200366079331962132411967917697877875277103045755972006084078559453777291403087575061382674872573336431876500128247133861957730154418461680506403680189755399752882558438393107151815794295272358955300914752523377417192504702798450787430403387076153
# 48757373363225981717076130816529380470563968650367175499612268073517990636849798038662283440350470812898424299904371831068541394247432423751879457624606194334196130444478878533092854342610288522236409554286954091860638388043037601371807379269588474814290382239910358697485110591812060488786552463208464541069

AI解法：
拿到题目后，我们手里只有n ，c ，e，但没有 p 和 q ，所以第一步就是分解 n。

  1. 先直接上 yafu / factordb
    （注意！！！分解时要求P*Q=N，且注意P跟Q的bit特征，在此题当中只有512bit）
1
2
p = 72224896773450610791657349018700642791668283264384520670702825479122904864127
q = 72224896773450610791657349018700642791668283264384520670702825479122904864239

（这两个数只差 112，所以 yafu 的 ECM / SIQS 都能秒破。）（yafu下载后卡死【待解决】

  1. 有了 p、q，就能算私钥 d
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from Crypto.Util.number import *
from gmpy2 import *

n = 52147017298260357180329101776864095134806848020663558064141648200366079331962132411967917697877875277103045755972006084078559453777291403087575061382674872573336431876500128247133861957730154418461680506403680189755399752882558438393107151815794295272358955300914752523377417192504702798450787430403387076153
c = 48757373363225981717076130816529380470563968650367175499612268073517990636849798038662283440350470812898424299904371831068541394247432423751879457624606194334196130444478878533092854342610288522236409554286954091860638388043037601371807379269588474814290382239910358697485110591812060488786552463208464541069
e = 65537

p = 72224896773450610791657349018700642791668283264384520670702825479122904864127
q = 72224896773450610791657349018700642791668283264384520670702825479122904864239

assert p * q == n
#校验等式是否成立

phi = (p - 1) * (q - 1)#欧拉函数
d = invert(e, phi)#e*d≡1mod phi
m = pow(c, d, n)
print(long_to_bytes(m))

（这题就是典型的“p、q 距离太近”导致用 Fermat 方法或 ECM 就能秒分解。）（这两个方法是什么？

· 来源：spc学长xc

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from Crypto.Util.number import *

m = bytes_to_long(b'flag{******}')

p = getPrime(512)
q = getPrime(512)
r = getPrime(512)
# 分别独立地生成 3 个 512 bit（≈154 位十进制）的随机强素数 p、q、r。这三个素数就是后面多素数 RSA 的因子。

h1 = 1*p + 1*q + 1*r
h2 = 2*p + 3*q + 3*r
h3 = 9*p + 9*q + 6*r
print( "hint_of_pqr=" , h1 , h2 , h3 )
# h1,h2,h3可求出pqr的值

e = getPrime(64)
# 生成一个 64 bit 的随机素数 e，用作 RSA 公钥指数。

a_big_prime = getPrime( 512 )
# 再生成一个 512 bit 的随机素数，起名叫 `a_big_prime`。
# 注意：这个名字有误导性，它并不是 RSA 模数 N 的因子，只是额外生成的一个素数，用来产生另一条“hint”（？什么鬼

hint = pow(a_big_prime,e,2**512)
#计算
# pow（a,b,c）=（a^b）%c
# 在 CTF 语境里，这往往暗示“partial key exposure”——低 512 位泄漏
# 攻击者可用 Coppersmith/Howgrave-Graham lattice 方法恢复完整私钥。
# 不过本题真正解密不需要它，因为 e 很小且 n 的因子我们已能求出。

print( "the big prime is: " , a_big_prime )
print( "hint is:" , hint )

n = p*q*r
# 构造一个 3 素数 RSA 模数 n，长度 3×512 = 1536 bit。
c = pow( m , e , n )
print( "c=" , c )
# 输出密文 c

'''
hint_of_pqr= 26205997351166240405785097231436009350807507606268828636742615246287109077466822241186639293389573242216311668227098054599788791116215571416316140409352427
66860315641471130491119218972922785980480599406983109647358601581641695642878472456945137024883369147959034865118793676633880997281324220353834323524635144 213473629205254382083617791480463504155040467378518856042962121442859026373709762896295778597714884481459316375098621436229734548467857563069831689551454946
the big prime is:  11557301053448817361014126921662226367639845395602185765021724910056663884113570410496382266851427507275779260616871464855286322325118092388982283547918921
hint is: 10271913433365953528187318472631779008104540530202414129752768330046395509900224800993688431964630907432047820727638055487310601524087956924122431108238505
c= 116569284047193403361251336983936346094224289856857789287062750599584928427772025697885153355908857327470083147465892652988245017837819503727301904206404536314951181113506280048949514352483259762138034268916332027429633274027588317302925270485836816591363962835119659624022139707163858477460375467148571163549410771927644341667962740112294140641187548649921303016157469076294782957230926056116058301134087751871726212821846406513780951057663400249479830993970711
'''

自己解出来了但方法过于复杂，无参考价值，所以只保留学长wp作为存档。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from Cryptodome.Util.number import long_to_bytes as l2b
import sympy

h1 =  26205997351166240405785097231436009350807507606268828636742615246287109077466822241186639293389573242216311668227098054599788791116215571416316140409352427
h2 =  66860315641471130491119218972922785980480599406983109647358601581641695642878472456945137024883369147959034865118793676633880997281324220353834323524635144
h3 =  213473629205254382083617791480463504155040467378518856042962121442859026373709762896295778597714884481459316375098621436229734548467857563069831689551454946
a_big_prime =   11557301053448817361014126921662226367639845395602185765021724910056663884113570410496382266851427507275779260616871464855286322325118092388982283547918921
hint =  10271913433365953528187318472631779008104540530202414129752768330046395509900224800993688431964630907432047820727638055487310601524087956924122431108238505
c= 116569284047193403361251336983936346094224289856857789287062750599584928427772025697885153355908857327470083147465892652988245017837819503727301904206404536314951181113506280048949514352483259762138034268916332027429633274027588317302925270485836816591363962835119659624022139707163858477460375467148571163549410771927644341667962740112294140641187548649921303016157469076294782957230926056116058301134087751871726212821846406513780951057663400249479830993970711
#解方程
p = 3*h1 - h2
r = (9*h1 - h3)//3
q = h1 - p -r

#解e
e = sympy.discrete_log(2**512,hint,a_big_prime)

#rsa算法
n = p*q*r
fain = (p-1)*(q-1)*(r-1)
d = pow(e,-1,fain)
m = pow(c,d,n)
print(l2b(m))